Giải toán 10, giải bài tập đại số 10, giải bài tập hình học 10 dễ hiểu

Cho tía vectơ (overrightarrowa), (overrightarrowb), (overrightarrowc) đều khác vec tơ (overrightarrow0). Những khẳng định tiếp sau đây đúng xuất xắc sai?

a) nếu như hai vectơ (overrightarrowa), (overrightarrowb) cùng phương với (overrightarrowc) thì (overrightarrowa), (overrightarrowb) cùng phương.

Bạn đang xem: Giải toán 10, giải bài tập đại số 10, giải bài tập hình học 10 dễ hiểu

b) Nếu (overrightarrowa), (overrightarrowb) cùng ngược phía với (overrightarrowc) thì (overrightarrowa) và (overrightarrowb) cùng hướng .

Giải

a) hotline theo đồ vật tự (Delta _1,Delta _2,Delta _3) là giá của những vectơ (overrightarrowa), (overrightarrowb), (overrightarrowc)

(overrightarrowa) cùng phương với (overrightarrowc) ( Rightarrow Delta _1//Delta _3) ( hoặc (Delta _1 equiv Delta _3)) (1)

(overrightarrowb) cùng phương với (overrightarrowc) (Rightarrow Delta _2//Delta _3) ( hoặc (Delta _2 equiv Delta _3) ) (2)

Từ (1), (2) suy ra (Delta _1//Delta _2) ( hoặc (Delta _1 equiv Delta _2) ), theo có mang hai vectơ (overrightarrowa), (overrightarrowb) cùng phương.

Vậy câu a) đúng.

b) Đúng.

Bài 2 trang 7 sgk hình học lớp 10

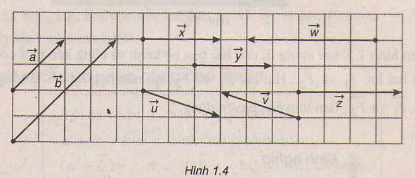
Trong hình 1.4, hãy chỉ ra các vec tơ cùng phương, cùng hướng, ngược hướng và những vectơ bằng nhau.

Giải

- các vectơ thuộc phương: (overrightarrowa) và (overrightarrowb); (overrightarrowx), (overrightarrowy), (overrightarrowz) và (overrightarroww); (overrightarrowu) và (overrightarrowv).

- những vectơ thuộc hướng: (overrightarrowa) và (overrightarrowb); (overrightarrowx), (overrightarrowy), (overrightarrowz)

- các vectơ ngược hướng: (overrightarrowu) và (overrightarrowv); (overrightarrowz) và (overrightarroww); (overrightarrowy) và (overrightarroww); (overrightarrowx) và (overrightarroww).

Xem thêm: Top Phim Mỹ Hay Nhất Mọi Thời Đại (Theo Xếp Hạng Trên Imdb), 40 Phim Mỹ Hay Nhất Mọi Thể Loại

- những vectơ bằng nhau: (overrightarrowx) = (overrightarrowy).

Bài 3 trang 7 sgk hình học tập lớp 10

Cho tứ giác (ABCD). Chứng minh rằng tứ giác chính là hình bình hành khi và chỉ khi (overrightarrowAB) = (overrightarrowDC).

Giải

Ta chứng minh hai mệnh đề:

*) Khi (overrightarrowAB) = (overrightarrowDC) thì (ABCD) là hình bình hành.

Thật vậy, theo định nghĩa của vec tơ đều bằng nhau thì:

(overrightarrowAB) = (overrightarrowDC) ⇔ (left | overrightarrowAB ight |) = (left | overrightarrowDC ight |) cùng (overrightarrowAB) và (overrightarrowDC) cùng hướng.

 (overrightarrowAB) và (overrightarrowDC) cùng hướng suy ra (overrightarrowAB) và (overrightarrowDC) cùng phương, suy ra giá của chúng tuy vậy song cùng với nhau,

hay (AB // DC) (1)

Ta lại có (left | overrightarrowAB ight |) = (left | overrightarrowDC ight |) suy ra (AB = DC) (2)

Từ (1) cùng (2), theo vệt hiệu phân biệt hình bình hành, tứ giác (ABCD) tất cả một cặp cạnh song song và bằng nhau vì thế nó là hình bình hành. 

*) lúc (ABCD) là hình bình hành thì (overrightarrowAB) = (overrightarrowCD)

khi (ABCD) là hình bình hành thì (AB // CD). Dễ dàng thấy, từ trên đây ta suy ra nhị vec tơ (overrightarrowAB) và (overrightarrowCD) cùng phía (3)

Mặt không giống (AB = CD) suy ra (left | overrightarrowAB ight |) = (left | overrightarrowCD ight |) (4)

Từ (3) cùng (4) suy ra (overrightarrowAB) = (overrightarrowCD).

Bài 4 trang 7 sgk hình học tập lớp 10

Cho lục giác rất nhiều (ABCDEF) gồm tâm (O).

a) Tìm những vec khổng lồ khác (overrightarrow0)và thuộc phương với (overrightarrowOA)

b) Tìm những véc tơ bởi véc tơ (overrightarrowAB)

Giải

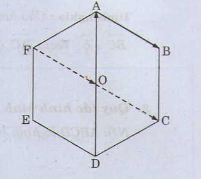
a) những vec tơ cùng phương cùng với vec tơ (overrightarrowOA):

(overrightarrowBC); (overrightarrowCB); (overrightarrowEF); (overrightarrowDO); (overrightarrowOD); (overrightarrowDA); (overrightarrowAD); (overrightarrowFE) và (overrightarrowAO).

b) Các véc tơ bởi véc tơ (overrightarrowAB): (overrightarrowED); (overrightarrowFO); (overrightarrowOC).