Giải bài tập toán hình 10 trang 12
Giải bài tập trang 12 bài xích 2 Tổng và hiệu của nhì vectơ Sách giáo khoa (SGK) Hình học tập 10. Câu 5: đến tam giác...
Bạn đang xem: Giải bài tập toán hình 10 trang 12
Bài 5 trang 12 sgk hình học tập lớp 10
Cho tam giác (ABC) cạnh (a). Tính độ dài của các vectơ (overrightarrowAB+ overrightarrowBC) và (overrightarrowAB- overrightarrowBC)
Giải
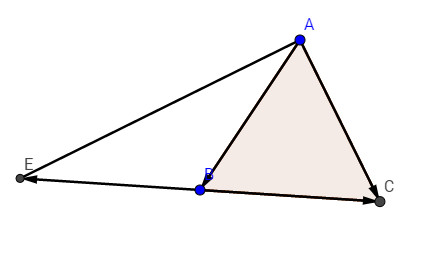
Ta có (overrightarrowAB+ overrightarrowBC= overrightarrowAC)
(left | overrightarrowAB+overrightarrowBC ight | = left | overrightarrowAC ight |= a)
Ta có: (overrightarrowAB - overrightarrowBC = overrightarrowAB +overrightarrowCB).
Trên tia (CB), ta dựng (overrightarrowBE = overrightarrowCB)
( Rightarrow overrightarrowAB - overrightarrowBC = overrightarrowAB +overrightarrowBE= overrightarrowAE)
Tam giác (EAC) vuông trên (A) (vì gồm đường trung con đường (AB) bằng nửa cạnh (CE)) bao gồm : (AC = a, CE = 2a) , suy ra (AE = sqrt CE^2 - AC^2 = sqrt 4a^2 - a^2 = asqrt 3 )
Vậy (left | overrightarrowAB -overrightarrowBC ight | = left | overrightarrowAE ight | = asqrt3)
Bài 6 trang 12 sgk hình học lớp 10
Cho hình bình hành (ABCD) tất cả tâm (O). Chứng minh rằng:
a) (overrightarrowCO - overrightarrowOB = overrightarrowBA);
b) (overrightarrowAB - overrightarrowBC = overrightarrowDB);
c) (overrightarrowDA -overrightarrowDB = overrightarrowOD - overrightarrowOC);
d) (overrightarrowDA - overrightarrowDB + overrightarrowDC = overrightarrow0).
Giải
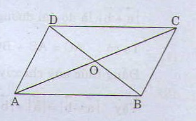
a) Ta có, theo quy tắc tía điểm của phép trừ:
(overrightarrowBA = overrightarrowOA- overrightarrowOB) (1)
Mặt khác, (overrightarrowOA = overrightarrowCO) (2)
Từ (1) cùng (2) suy ra:
(overrightarrowBA= overrightarrowCO - overrightarrowOB).
b) Ta gồm : (overrightarrowDB= overrightarrowAB - overrightarrowAD) (1)
(overrightarrowAD = overrightarrowBC) (2)
Từ (1) và (2) mang lại ta:
(overrightarrowDB = overrightarrowAB- overrightarrowBC).
c) Ta có :
(overrightarrowDA - overrightarrowDB = overrightarrowBA) (1)
(overrightarrowOD - overrightarrowOC = overrightarrowCD) (2)
(overrightarrowBA = overrightarrowCD) (3)
Từ (1), (2), (3) suy ra
(overrightarrowDA -overrightarrowDB = overrightarrowOD - overrightarrowOC) đpcm.
d) (overrightarrowDA - overrightarrowDB + overrightarrowDC = (overrightarrowDA - overrightarrowDB) + overrightarrowDC)
(= overrightarrowBA+overrightarrowDC = overrightarrowBA+ overrightarrowAB= overrightarrow0) ( vì (overrightarrowDC= overrightarrowAB) ).
Xem thêm: Thuê Dịch Vụ Vệ Sinh Nhà Cửa, Dọn Dẹp Nhà Ở Tphcm 10K/M², 55K/Giờ
Bài 7 trang 12 sgk hình học tập lớp 10
Cho (overrightarrowa), (overrightarrowb) là nhị vectơ khác(overrightarrow0). Khi nào có đẳng thức
a) (left | overrightarrowa+overrightarrowb ight | = left | overrightarrowa ight |) + (left | overrightarrowb ight |);
b) (left | overrightarrowa+overrightarrowb ight |= left | overrightarrowa-overrightarrowb ight |).
Giải
a) Ta tất cả (left | overrightarrowa+overrightarrowb ight | = left | overrightarrowa ight |) + (left | overrightarrowb ight |)
Nếu coi hình bình hành (ABCD) có (overrightarrowAB = overrightarrowDC= overrightarrowa) và (overrightarrowAD= overrightarrowBC= overrightarrowb) thì (left | overrightarrowa+overrightarrowb ight |) là độ nhiều năm đường chéo cánh (AC) và (left | overrightarrowa ight |= AB); (left | overrightarrowb ight |= BC).
Ta lại có: (AC = AB + BC)
Đẳng thức xảy ra khi điểm (B) nằm trong lòng hai điểm (A, C).
Vậy (left | overrightarrowa+overrightarrowb ight | = left | overrightarrowa ight |+ left | overrightarrowb ight |) khi hai vectơ (overrightarrowa), (overrightarrowb) cùng hướng.
b) Tương tự, (left | overrightarrowa+overrightarrowb ight |) là độ lâu năm đường chéo (AC)
(left | overrightarrowa-overrightarrowb ight |) là độ dài đường chéo cánh (BD)
(left | overrightarrowa+overrightarrowb ight | =left | overrightarrowa-overrightarrowb ight |) (Rightarrow AC = BD).
Hình bình hành (ABCD) bao gồm hai đường chéo cánh bằng nhau vì thế nó là hình chữ nhật, ta bao gồm (AD perp AB) hay (overrightarrowaperpoverrightarrowb).















